olzheritage.blogg.se

Not all variables need to be entered into the table. The first column is the variable name and the second column is the corresponding variable label.

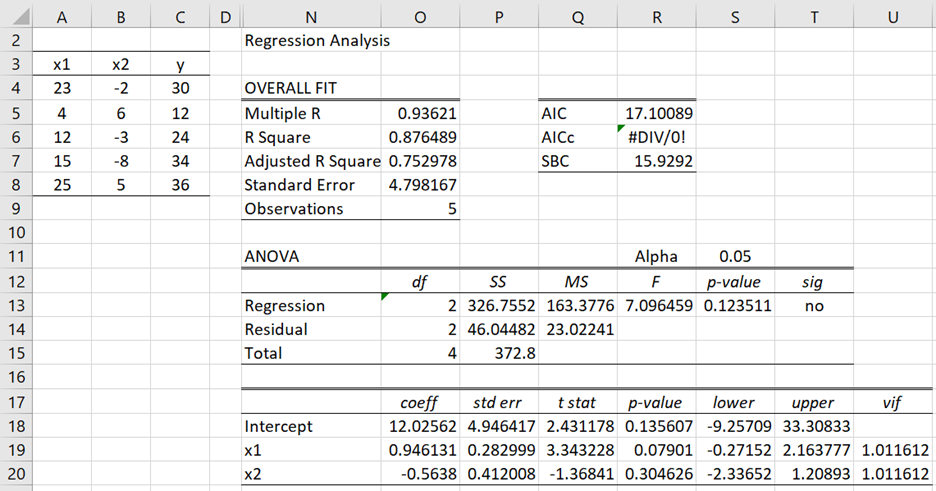
Create the table formatted as two columns. 90 71 87Īs an option, also read the table of variable labels. # 5 JobSat character 35 2 3 med low high. # 3 Dept character 36 1 5 ADMN SALE FINC. # Name Type Values Values Values First and last values # double: Numeric data values with decimal digits # integer: Numeric data values, integers only It is rarely useful, and easy to overinterpret.# Details about your data, Enter: details() for d, or details(name) If you force the line through the origin, be very wary when interpreting the P value. Usually this option is used to fit calibration curves used for interpolation, in which case the P value is not useful. Given the constraint that the line must go through the origin (X=0, Y=0 lower-left of graph), the data are quite convincing that best fit line is far from horizontal, so it makes sense that the P value is tiny.Ĭonstraining a line to go through the origin (or some other point) can be very useful in some situations. Since the line is far from horizontal, the P value is tiny. To make the line go through the origin and also go near the points, the best-fit line has a slope is far from zero.

The results are very different when you fit linear regression with the constraint that the line has to go through the origin (blue line). The P value, from conventional linear regression fitting both slope and intercept, will be small only when the points form a linear pattern that is not horizontal. Some people are confused and think the P value should be small purely because the points for a pattern. Since the observed slope is zero, there is almost a 100% chance of observing a slope that is further than zero than observed! So the P value is greater than 0.99, as high as a P value can be. The P value answers the question: If the true slope is zero, what is the chance that the slope will be further from zero than the observed slope due only to random sampling.

When fit with linear regression the usual way (fit both slope and intercept green line), the best fit value of the slope is 0.00. The data points almost form a horizontal line. The graph below demonstrates the problem: Beware of the P value from linear regression when you force the line to go through the origin or some other point.